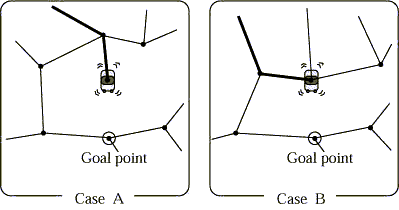
Figure 18: Dijkstra 法に対する代替法の問題点 ´
ここでは,Dijkstra のアルゴリズムを使わずに,スタート地点から ゴール地点までの経路を導くための簡単でかつ不完全な方法を示します.
練習問題 3-2 まで出来た人は与えられた経路に沿って移動体を 動かすことが出来ました.しかし,このプログラムでは 隣接する交差点を与えなくてはなりません. 結局人間が経路を決めている訳ですからこれをカーナビゲーションと呼ぶには あまりにお粗末です.そこで,せめてスタート地点とゴール地点を入力するだけで ゴール地点までの経路を決定するプログラムを作成してみましょう.
与えられるのはスタート地点とゴール地点だけです. したがって,最初の問題はスタート地点から次に進む交差点を決定することです. 隣接する交差点とその位置はわかりまから,ゴール地点との直線距離 が一番小さい交差点を選ぶのは妥当な戦略ですね. これを繰り返すと運が良ければゴール地点に到達することができます. しかし,図18 に示すように袋小路に入ってしまったり,別のところに極小点が あると抜け出せなくなります.
どうすればよいでしょう?
ここから先は皆さんの工夫次第です.図に示すような状態になっても
ゴール地点までたどりつけるアルゴリズムを考案して下さい.
´
Figure 18: Dijkstra 法に対する代替法の問題点 ´
-----------------------
#ifndef _Xtc_h
#define _Xtc_h
typedef enum {
NONE, TGIF } term_type;
extern FILE *TGIF_outfile;
/*
* Xtc header
*/
#define SCREEN_WIDTH 640
#define SCREEN_HEIGHT 400
enum color_macros {
BLACK, BLUE, GREEN, CYAN, RED, MAGENTA, BROWN, LIGHTGRAY,
DARKGRAY, LIGHTBLUE, LIGHTGREEN, LIGHTCYAN, LIGHTRED, LIGHTMAGENTA,
YELLOW, WHITE, NCOLORS, };
enum graphics_functions {
COPY_PUT, XOR_PUT, OR_PUT, AND_PUT, NOT_PUT, };
enum line_sytles {
SOLID_LINE, DOTTED_LINE, CENTER_LINE, DASHED_LINE, };
enum line_widths { NORM_WIDTH = 1, THICK_WIDTH = 3, };
void arc(), bar(), circle(), cleardevice(), closegraph(), drawpoly(),
ellipse(), fillellipse(), fillpoly(), getimage(),
initgraph(), line(), linerel(), lineto(), moverel(), moveto(),
outtextxy(), pieslice(), putimage(), putpixel(), rectangle(),
sector(), setbkcolor(), setcolor(), setlinestyle(), setrgbpalette(),
setwritemode();
int getbkcolor(), getcolor(), getmaxcolor(), getmaxx(), getmaxy(),
getpixel(), getx(), gety(), imagesize(),
textheight(), textwidth();
int cur_pointer_x, cur_pointer_y;
void xtcmainloop(), xflush();
int xgetbutton();
#endif /* _Xtc_h */
-----------------------