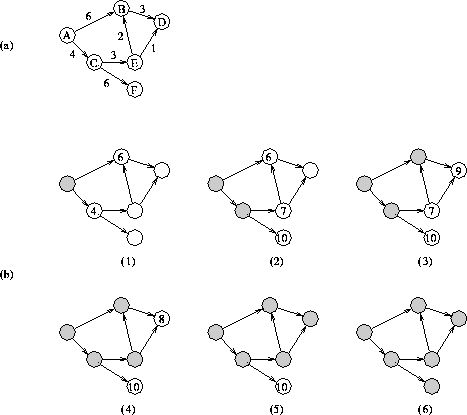
Figure 15: Dijkstra のアルゴリズムの動き
このアルゴリズムの動き方の例を図 15 に示す.同図(a)の グラフ(数字は辺の重み,Aが出発点)にアルゴリズムを適用すると,(b)の順 序で各頂点までの最短路を確定していく.陰のついているのが最短路の確定し ている頂点である.頂点の中の数は,その時点までにわかっているその頂点へ の最短の道の長さを表す.各ステップでは,この値が最小の頂点を選んで,最 短路を確定している.頂点Dの値が(3)と(4)の間に変わっている点に注意する こと.

Figure 15: Dijkstra のアルゴリズムの動き
出発点からの最短距離が確定している頂点の集合を V,未確定の頂 点の集合を U と呼ぶことにしよう.集合 U に含まれる各頂 点には,出発点から V に属する頂点だけを経由してその頂点に到達 する最短の道の長さを与えておく (図15 の頂点内の数). ここでは,これをその頂点のフィールドdistanceに記録するものとする.出 発点からの道がまだ見つかっていない頂点のフィールドdistanceには,ここ で∞と名付ける特別な値を与える.これはあらゆる道の長さよりも大 きな値を選べばよい.
アルゴリズムの実行途中では,各頂点のフィールドdistanceの値が真の最短 路の長さに等しいとは限らない.しかし, U の中でdistanceの値 が最小の頂点に関しては,このときのdistanceの値が出発点からの最短路の 長さである.こう決めてよい理由は後で述べる.この頂点への最短路はこの時 点で確定できるので,これを U から V に移してよい. これがDijkstraのアルゴリズムの基本操作である.
アルゴリズムの初期状態は,すべての頂点が U に入った状態である. このとき,フィールドdistanceの初期値は,出発点で0,出発点以外で ∞である. この状態から上記操作を繰り返し適用して, 全頂点が V に移ったらアルゴリズムは終了である.
フィールドdistanceの値の更新は頂点( p とする)を U から V へ移すときに行う. U の各頂点( q とする)について, p を経由して q に至る道の長さ( p までの最短路の長さと p → q の辺の重みの和)が,それまでに得られた q までの最短路 よりも短いかどうかを調べる.もし短いようなら,頂点 q のフィールド distanceをこの値で書き換える.
以上のアルゴリズムを疑似アルゴリズムの形で書くと次のようになる.
procedure ( dijkstra; )
var (U, V:) 頂点の集合;
begin
V:=空集合;
U:=すべての頂点からなる集合;
vertex[出発点].distance:=0;
for x:=出発点以外のすべての頂点について do
vertex[x].distance:= ∞;
while Uが空集合でない do
begin
p:=Uの中でフィールドdistanceの値が最も小さい頂点;
pをUから除き,Vに加える;
for p を始点とする辺それぞれについて do
begin
x:=辺の行き先の頂点;
if x が U に属している then
vertex[x].distance:=
min(vertex[x].distance, vertex[p].distance+辺の重み);
end;
end;
end;
アルゴリズム終了時の各頂点のフィールドdistanceの値が出発点からの最短 路の長さである.
Dijkstraのアルゴリズムで最短路が正しく求められる理由は次の通りである. まず,U 内の各頂点のフィールドdistanceには,V に属 する頂点だけを経由してその頂点に達する最短の道の長さが常に記録されてい る.これはアルゴリズムの作り方から容易に確認できる.したがって集合U の中でフィールドdistanceの値が最小の頂点 p を選んだときに, p ま での最短路が V に属する頂点しか経由しないことを証明すればよい. これが正しければこの時点で p までの最短路の長さ(フィールド distanceに計算済み)を確定できる.1ステップに1頂点ずつ最短路の長さを 確定していけば,nステップでアルゴリズムは終了する.
p までの最短路が V に属する頂点だけを経由することは次のよう に証明できる.V に属しない頂点を経由して p に至る道があり, V から直接 p に達する道より短いものとする(図 16 の破線).この道の上で V の外にある.(出発 点から見て)最初の頂点を q とする.このとき, q から p までの道 の長さは,正または0であるから,出発点から V に属する頂点だけを 通って q に至る道の長さは,同じく p に至る道の長さより短くなくては ならない.しかし,これはありえない.この長さが最短のものを選んで p としたのだから, p に至る道は q に至る道よりも短い(または等しい) はずである.したがって, q を経由して p に至る道の方が短いという仮 説は誤りである.
以上の説明からわかるように,Dijkstraのアルゴリズムが正しく動くためには, 辺の重みが負でないことが本質的である.負の重みを持つ辺があれば,頂点 p までの最短路が U に属する頂点(たとえば q )を経由しないとは 保証できない.
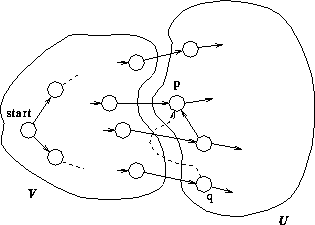
Figure 16: Dijkstra のアルゴリズムの正しさの証明
(以上、岩波講座ソフトウェア科学 3.アルゴリズムとデータ構造より抜粋)
なお,ここでは有向グラフの例を用いていますが,本アルゴリズムは無向グラ フにおいても有効です. 図 17 にPADを用いたDijkstra のアルゴリズムを示します. プログラム作成時の参考にしてください.
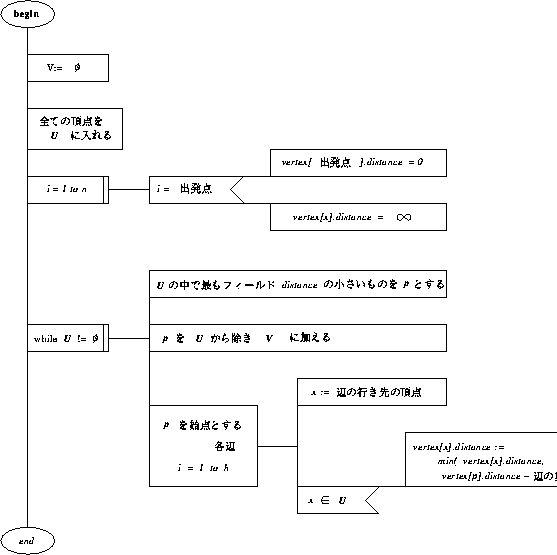
Figure 17: PAD による Dijkstra のアルゴリズムの表現
練習問題 4-1
これまでに作成した道路情報を元に,2点間の最短路を求め,それを表示させ るプログラムを作りなさい.
練習問題 4-2
同様に最短時間で目的地に到着する経路を求めそれを表示させるプログラムを 作成しなさい.またその経路に沿って移動体が動く様子を視覚化しなさい.
練習問題 4-3
道路情報(混み具合等)が時間とともに変化するように定め,一定時間ごと (あるいは交差点ごと)に現在地から最も早く目的地までに到着できる経路を 表示させ,それに沿って移動体が動くプログラムを作成しなさい.