研究概要

研究課題

科学研究費補助金　基盤研究 (Ｓ)
研究課題番号：25220702　
研究課題名：「数理モデルにおける非線型消散・分散構造の臨界性の未開領域解明」
研究代表者： 小川　卓克
日本学術振興会のページ

本研究の主旨

様々な分野の数理モデル(物理学、生物化学、天文学、電子工学、プラズマ工学など)で非線形連立偏微分方程式として定式化される問題のうち、臨界性にまつわる非線型現象を、内在する「消散性」と「分散性」に着目して解析学の精緻な手法で研究し、「臨界構造」の背後にある未開の非線型的数理を探求するのが目的である。

研究題材は非線形の連立型偏微分方程式を中心とするが、その周辺の数理モデルや微分幾何学に源泉をもつ偏微分不等式・方程式や幾何学的変分問題、あるいは非線形差分方程式なども総合的に研究対象とする。

特に自然現象をあらわすモデルが、しばしば臨界性を提示し、さらに臨界時にモデルが安定化する傾向の本質的な理由を探る。

研究の背景

典型的な例として15年ほど前まで、コルテベーグ・ド・フリース方程式(KdV方程式) のように代数的に可解な方程式を、解析学の手法で、非常に一般的な初期値に対する可解性を証明することは困難に思われていた。

しかし1993年以降の10年間に、BourgainやPonceらによる研究によって、 delta 測度を含む広範な超函数の空間において、時間大域的に方程式が一意的かつ安定に解けることが示されている。 こうした問題を「適切性の問題」と呼ぶが、KdV 方程式の適切性解決の原動力に、 実解析の分野で大きな業績を上げている研究者らが含まれている点は注目できる(J. Bourgain, T. Taoなどいずれもフィールズ賞受賞者)。

この理論の波及効果として、必ずしも完全可積分とは限らない問題に対して、同様の適切性理論が適用可能になりつつある。

一方、Poincare予想解決のシナリオにRicci 曲率流による3次元多様体崩壊の議論があるが、それは非線形偏微分方程式論で培われた技法が重要な位置を占めている。

そこでは非圧縮性 Navier-Stokes 方程式などの解の正則性理論で重要な「エプシロン-正則性理論」が応用されており、 そうした議論にwavelet展開の技法を援用すると、より広範な偏微分方程式の解に対する正則性定理を構築できる可能性がある。

国内の研究者らの動向との関連

そこで、実解析学固有の有効な手段をうまく取り入れることにより蓄積を呼び起こすことが可能である。 実際、Lettlewood-Paley 流の技法をNaveir-Stokes 方程式に適用して、正則性理論の改善や判定条件を与える例や、 回転する障害物のまわりの研究などに適用して成功した例があり、従来の研究も伝統的に実解析的手法に基づいていたがゆえに有効に働く兆候が見える｡

また解の解析性という観点からは、複素方向への波の位相の干渉を取り入れた研究が今後有効となることが我々の研究から判明しつつある。

本研究で明らかにしたい点と予想される効果

本研究では、非線形偏微分方程式で表される数理モデルに対して、 実解析学の精密な議論や複素解析学からの技法を援用して、 理解の範囲と深さを高めることを目指す。

上記のごとく、研究の深化とその理解の容易さは常に背反する問題であるが、それを比較的容易にするのは、 単純でしかも本質をえぐり出す効果的な具体例を提示することにある。 数理物理(あるいは生物化学)のモデルの中にはそれに適した題材が数多く存在する。

たとえばタマホコリカビの胞子形成には自己組織化とともに球面形成構造が隠されており、 密度の凝集には等周不等式の最良定数に関わる量8πが寄与する。

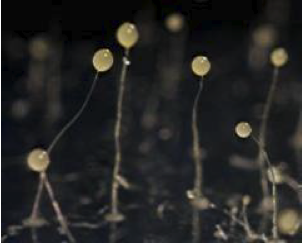
タマホコリカビの胞子形成

こうした例に現れるように、微分方程式固有の技法にとどまらない汎用性の ある理論の発見は、実解析学者、確率解析学者、微分幾何学者に与えるインパクトも大きい。

申請者は, ここ6-7年ほど臨界型非線形偏微分方程式についてそれらの形式にこだわらずに、 その共通する性質を探り出すことに従事してきた。 そこではLittlewood-Palay理論や偏微分方程式に即した実解析的手法が大きな効果をもたらすことを経験した。 それはあたかも擬微分作用素の理論が線形偏微分方程式に果たした役割を、 非線形問題にうまく適用させるがごとくの観がある。

実際、残念ながら擬微分作用素を用いる技法のみでは、 こうした臨界型の問題で必ず損失を生じて解析できない。

従って非線形理論に汎用的に適用可能な擬微分作用素の対応物を実解析学の 援用と深化によって得ることは、本研究には不可欠である。

一方、本課題が目指す問題の背後に、モデルが元々備える消散性・分散性と 非線型性の拮抗がもたらす臨界性が特異的に働くことは、 これまでの研究により明らかになっている

一般に臨界状況においては、消散性と分散性が共に系を安定化させる 方向に寄与し、非線形問題のタイプに依存しない傾向がある。 臨界性とは非線型効果と線型安定効果の拮抗の産物ではあるが、 臨界性の所以から解析的にぎりぎりの評価を伴いそれを 得るためには、 大域解析的な偏微分方程式の解構造の 把握が大いに寄与する。その際、モデルに自然に備わるエネルギーや エントロピーから生成される変分汎函数の(無限次元)幾何構造の 解明が重要な役割を担う。

変分汎函数の最急降下方向への幾何が時間大域挙動に直結する 非線型熱方程式ではそうした研究が進んでいるが、 保存則を持つハミルトン系である物理モデルは拘束条件付きの 変分問題となり、大域挙動は消散型のそれとは大いに異なる。

こうした変分構造の違いと、にもかかわらず双方とも同様な 臨界安定性を示す断片的な結果の齟齬は 本質的にこうした大域構造の理解が進んでいないことの表れである。

こうしたモデルの変分構造を理解することが本課題の重要な視点である。 臨界性を有する問題では、非線形効果と消散・分散効果が 相補的に系を安定化させる傾向を持つように思われる。

この部分を明快にし、モデルの臨界性の数学的構造を知ることが 本課題の最大の目標であり研究が進展すれば周辺の数理において 臨界状況を超えた解析学的に未開の分野を切り開く出発点となる。

本研究の総合性と周辺分野からの寄与

本課題には広範な分野からの寄与を期待している。 実解析学と微分幾何学および確率解析からは 分野の中にとどまらない研究を生み出す可能性が強いが、 とりわけ、分岐過程に関する 確率論的な技法の微分方程式としての理解、さらに 実解析学を用いた展開が望まれる。 一例ではあるが、最近の非線形分散型方程式の 雑音摂動による確率解析など、実解析学と確率解析と 偏微分方程式が有機的に組み合わさって初めて証明できる 様々な問題が多く残されている。これらに スポットライトを当て、臨界性の理解に斬新な視点を 見いだすことは本研究で重視する点である。

研究の特色・意義と位置づけ

本課題実施に際して特に重視したい要因を二点挙げる。

第一には、偏微分方程式論で重要な臨界型函数不等式の発見と 応用である。実解析の精密な不等式が一つ発見されるたびに, 偏微分方程式論で重要な成果が生まれるといっても過言では ないであろう。

ここではそうした汎用不等式の中でも特に 臨界型のSobolev不等式、特に実補間空間論から派生する、 対数関数を制御するSobolev 型の不等式 (Grossの不等式と Brezis-Gallouetの不等式) および、その 双対と考えられる、Trudinger-Moser 型の不等式などの 詳しい研究を行う。そして自然な発展として、定数係数の 線形偏微分方程式に対する消散-分散型評価 (いわゆる Lp-Lq 型評価 あるいはStrichartz-Brenner評価) を Orlitz空間を用いて精密化する。 そこではこれまでの研究に加えて、非線型評価に効果的な双線形評価など、より精密な評価が要求される。

第二に、非線形問題の背後にある偏微分方程式論の大域的構造、特に 大域幾何構造の解明を行う。非線形双曲型方程式における零条件など、 幾何学的背景をもつ問題を解析学の言葉に焼き直し、その効果を 解析的な不等式として表現する。さらに いわゆる発散-回転ベクトル場に おける双補的発散-回転補正定理(divergence-curl lemma) などを典型に、 幾何学的背景をもつ解析的な手法の解明と探索は、 精密な議論を要求する非線形問題において非常に 強力である。

研究の背景・目的

多くの数理モデルは物理量の相互作用による非線型偏微分方程式で記述され、偏微分作用素による「線形構造」と、物理量の干渉に起因する 「非線型構造」を含む。 線形構造は消散構造(散逸構造)や分散構造に基づき、系の安定化に寄与し、物理量の干渉による非線型構造は系を非安定化に導く。 これら「線型・安定」構造と「非線型・不安定」構造がつり合う問題を「臨界問題」と呼び本研究の中心的対象となる。

数学的にも応用上も重要な多くの問題で、こうした臨界状況が発生し、興味深い数学的現象が現れる。また臨界状況では解析学的に主要な技法である「摂動法」が そのままでは通用しないため解析学的な研究はより困難となる。

本研究はこうした臨界性にまつわる問題を研究し、その背後に残されている未開領域ともいえる優臨界問題への足がかりを築くことにある。

研究の方法

本研究では、とりわけ臨界型ソボレフ不等式、対 数関数を制御するグロスの不等式、ブレジス-ガローエの不等式、および、その双対版と考えられるトゥルディンガー・モーザー型不等式の精密な研究を行う。そして自然な発展として、定数係数の線形偏微分方程式に対する消散-分散型評価(Lp-Lq型評価あるいはストリッカーツ・ブレンナー評価) をオルリッツ空間を用いて精密化する。

期待される成果と意義

様々な臨界問題の背後にはミレニアム問題として著名な問題を始めとして、重要な未解決問題が軒を連ねる。とりわけ重要な課題として分散性と消散性が同時に存在するモデルにおける解析で、従来、分散性と消散性の解析が互いに相殺し、数学的な証明が困難に陥って、一方の構造をもつ場合に及ぶ成果が得られなかったが、本研究により様々な問題における消散分散構造の分離と非線形干渉による効果の分類が明らかになるにつれて、こうした困難さが解決されるものと考えられる。また臨界函数不等式の確立に伴い、消散・分散効果を伴った様々な解析学的評価群(双線形・三重線型評価、 線型消散型評価・線型分散型評価・最大正則性原理) を確立し手法を磨き上げる