モアレパターン

モアレ(moiré¹)は一般に周期的な構造が互いに干渉するときに生じる新たなパターンであり、干渉の際のわずかなずれによりパターンが大きく変化する。このことは、多くの精密測定の測定原理にも用いられている一方で、微細加工の分野でモアレは位置合わせやプロセス精度が不十分だと生じる厄介者でもり、その抑制のために厳密な加工精度が求められる。いろんな場面に現れて一見、捉えどころのないモアレパターンであるが2次元周期系に生じるモアレは、あとで見るようにある種のベクトル場を形成し、それはトポロジカルに安定な性質を示す。このベクトル場を電磁場へ転写することができれば周期的に並んだトポロジカルチャージを持つ光（光渦）の生成など独自の空間変調素子へと展開できる可能性がある。本研究ではモアレと電磁場をつなぐ役割としてメタ表面に注目した。メタ表面は、2次元的に構造を作製、分布させることで物質表面（界面）の光学的特性を制御する。金属周期構造により電磁波との結合を担保し、その作成時にわずかなずれを導入することで構造パラメータにモアレによる分布を付加できる。このようなモアレ型メタ表面において、モアレの持つトポロジカルな性質の電磁場への影響を探ることを目的とする。

2次元モアレパターン

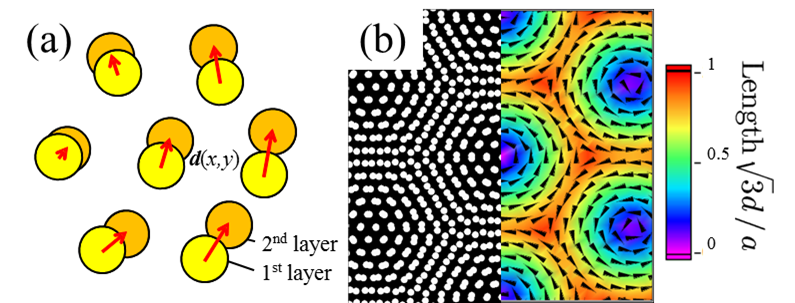
2つの二次元周期構造を重ね合わせてできるモアレパターンについて、より定量的に可視化するためにずれのベクトルを導入した。重ねる二次元周期構造のうち1層目のある格子点から2層目にある格子点のうち最近接の格子点に向かったベクトルを2次元面内で定義する(図2(a))。2つの層にずれを加えて重ねた場合、モアレが生じ、ベクトルは格子点の位置によって向きが異なり空間的な分布をもった「ベクトル場」を形成する。図2(b)に、二次元三角格子上に金属円盤を配置しわずかに回転させて重ねた場合のモアレパターン（左半面）およびベクトル場（右半面）を示す。この回転モアレのベクトル場を見たとき、方向が定められない特異点が2種類ある。１つめは図中青紫色のところで、ここでは2層の格子点同士の位置が一致しておりベクトルの長さはゼロとなっている。この点の周縁において、ベクトルの方向が1回転している。また、この特異点が３つ隣接する中央にもう一種類の特異点がある。その周囲ではベクトルが正味1/2回転している。回転以外のずらし方でも同様の特異点を見つけることができ、特異点の周りのベクトルの回転数はずらし方によらない普遍的な性質を持ち、それぞれをトポロジカル数l=1,-1/2の特異点として特徴づけることができる。

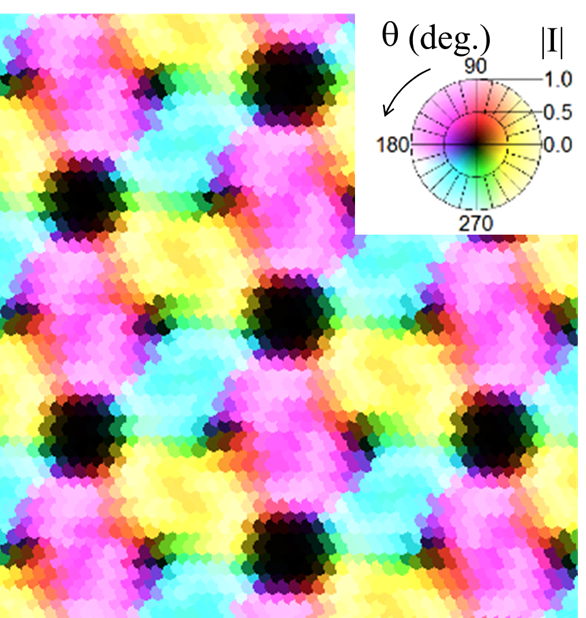
電磁場に現れる位相特異点

メタ表面の開発においてマクスウェルの方程式を数値的に解く電磁界シミュレーションは有用であるが、モアレ型メタ表面のモデル化を考えると、全体をそのままモデル化するには膨大なリソースが必要となり現実的ではない。そこで微小ずれ近似のもと、ずれの大きさが十分に小さい場合、局所的な応答は、ずれベクトルの異なる位置からの影響を受けないとした。これにより局所応答の計算に周期的境界条件が適用できる。モアレ型メタ表面の応答を得るためにまず、ずれベクトルdを計算パラメータの一つとし、xy面内において徐々にかえて計算した結果を保持しておく。次に回転ずれ角θ=0.05rad.のモアレ型メタ表面が作るずれベクトル場に対して、各位置におけるずれベクトルdを求めそれに対応する計算結果を対応させモアレ型メタ表面全体の光学応答を再構築した。それにより得られた円偏光クロスニコル測定における透過光の光学応答の面内分布を図3に示す。ずれのベクトル場において、特異点のあった箇所は分布において透過強度はゼロとなっている。トポロジカル数l=1,-1/2の特異点の周囲での位相の変化は、それぞれ4π,-2πとなっており、トポロジカル数に対応している。この性質は基本格子による回折限界以下の周波数領域で保存していた。これは、ベクトル場に生じた幾何学的特異点が光の場の位相特異点として現れていることを表しており、この性質に波長依存性がないことはトポロジカルな性質が現れているものである。

謝辞

本研究は、千葉大学・尾松孝茂先生、宮本克彦先生、情報通信研究機構・黒澤裕之博士、福岡大学・中山和之先生、理化学研究所・南出泰亜博士、Zhengli Han博士との有意義な議論の上になされた。本学・石原照也先生および同研究室メンバーより多角的な指摘を頂いた。

Funding

• 2016年度公益財団法人住友電工グループ社会貢献基金.
• 2017年理学研究科若手研究者奨励研究基金.
• JSPS Grant-in-Aid for Young Scientists (B) No. 24760035.

論文

• Seigo Ohno, “Projection of phase singularities in moiré fringe onto a light field,”
  Applied Physics Letters 108, 251104 (2016) doi:10.1063/1.4954709.