ダイクストラアルゴリズム


ダイクストラ法を完全に理解しているかどうか確認したい人は是非チャレンジして欲しいと思います。

目次

  1. 経路探索の対象とするグラフ
  2. ダイクストラ法による経路探索の例
  3. レポート課題
１. 経路探索の対象とするグラフ

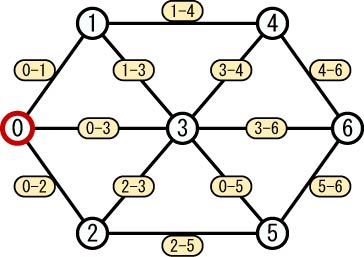
　ここでは、図1に示すような7ノードからなるグラフを経路探索の対象とします。
ノードはカーナビゲーション地図中の交差点に相当します。ノードは丸で表されて
おり、中にノード番号が書いてあります。ノード0は目的地で、ここではノード0か
ら各ノードへの最短経路距離を求めます。

　楕円で囲まれた記号は、ノード間を結ぶエッジを表します。エッジは地図中の道
路に相当します。(0-1)は、ノード0とノード1を結ぶエッジです。



図.1 経路探索の対象とするグラフ

*この図、エッジ(3-5)が(0-5)と間違っていますね...。すみません。

２. ダイクストラ法による経路探索の例

　各エッジの長さ(ノード間距離)を次のように決めた時の、ダイクストラ法による
最短経路距離探索の手順を以下に示します。この例では、７ステップで探索が終了
します。
　　　(0-1)　　　　3　　　　(0-2)　　　　4　　　
　　　(0-3)　　　　5　　　　(1-3)　　　　6
　　　(1-4)　　　　4　　　　(2-3)　　　　4
　　　(2-5)　　　　4　　　　(3-4)　　　　1
　　　(3-5)　　　　2　　　　(3-6)　　　　4
　　　(4-6)　　　　5　　　　(5-6)　　　　1


　白と水色(緑？)のノードは、最短経路距離が未定であることを表します(テキストで
いうところの集合U)。赤のノードは最短経路距離が確定しています(集合V)。ノードの
横に黒で書かれた数字は、その字点で分かっているそのノードまでの最短経路距離です。

　ステップを順に追いながら、ダイクストラ法による最短経路距離探索の手順を確
認しましょう。

ダイクストラ法のアルゴリズム(下記アルゴリズム1〜3が1ステップとなります) 
0. 全てのノードの、ゴールまでの距離を無限大(or 非常に大きな値)に初期化する
   ただし、ノード0のゴールまでの距離を0としておく(明らか)

1. 未確定ノードの中から、ゴールまでの距離が最小のノードを新たに確定する
   確定済ノード(赤)に隣接していないノードは無限大の距離を持つため、自然と確定済ノード(赤)に隣接するノード(緑)　　
   の中から、確定することになる

2. 確定したノードａに隣接する全てのノードｂiに対し、次のようにしてゴールまでの距離を更新する
    1) ｂiが確定済のノードなら何もしない
    2) 確定ノードａのゴールまでの距離と、ノードａとノードｂi間の距離を足した値を算出し、これをｄとする
    3) ｄがノードｂiに設定されているのゴールまでの距離よりも小さい場合、ｄをｂiのゴールまでの距離にする

3. 全てのノードが確定したら終り。そうでなければ1へ戻る


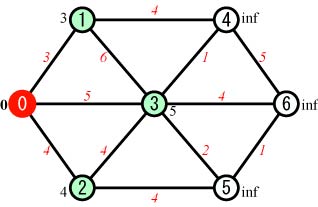Step.1

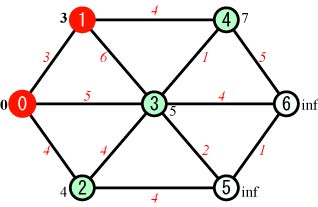Step.2

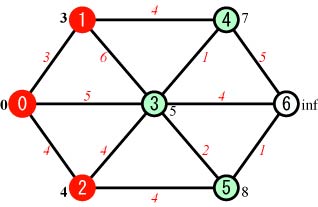Step.3

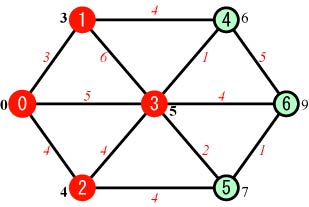Step.4

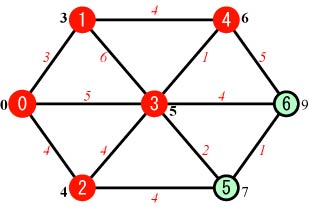Step.5

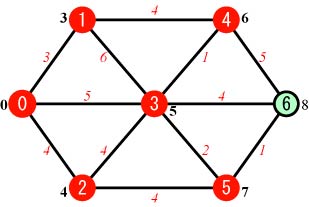Step.6

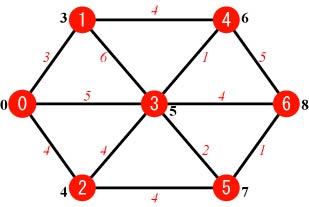Step.7

３. レポート課題