figure1
反陽子ヘリウム原子のエネルギー準位の精密計算

東北大・理 木野康志


1. はじめに
反陽子(p)は通常物質中に打ち込まれるとps程度の間に消滅するが、山崎・早野らは、ヘリウム中に打ち込まれたpのうち約3パーセントが、その106倍も長い寿命（数μs）を持つことを発見した。 打ち込まれたpはヘリウム原子をイオン化しながら減速し、エネルギーがイオン化エネルギー以下に達すると、pはヘリウム原子中の束縛電子と入れ替わり、中性の反陽子ヘリウム原子( pHe+= p+He2++e- )の３体系を形成する。この過程はpの軌道（エネルギー）が、1s電子のそれと等しいときに最も起りやすいため、主量子数は、1.jpgと非常に大きな数になる。このうちp−He2+間に大きな角運動量（Ｊ >30）を持つ状態は、大きな遠心力障壁のため、pの核による吸収・対消滅を免れる。また速いAuger過程による遷移は電子に大きな角運動量（ｌe >4）を与える必要があるため起こりにくいため、pHe+3体系は遅い電磁崩壊で遷移する準安定状態をもつ。
pHe+の準安定状態では、pは大きな角運動量をもつため円軌道に近い軌道をもち、電子は主に1s軌道に分布するがpとの間の斥力によりわずかに分極する(図1.)。pHe+3体系は相互作用の面からは、He2+(Z=+2)の周りをp(Z=-1)とe-(Z=-1)が回る「ヘリウム原子的」な描像が成り立ち、同時に動力学の面からは、圧倒的に重いヘリウム原子核とpの周りを軽い電子が回る「2原子分子的」な描像が成り立つ。この様にpHe+は原子と分子の特徴を合せ持つため、「アトムキュール( atomcule = atom + molecule )」と呼ばれる。我々はこのpHe+の特殊な性質を効果的に取り入れるため「非断熱組替えチャネル結合変分法」を用い精度の高い計算を行った。

2. 非断熱組替えチャネル結合変分法
565.jpg

figure12

「原子的描像」「分子的描像」および「電子−反陽子相関」を同時にかつ直接計算に取り入れるため、全波動関数48.jpgを図2.に示す3つの座標系でそれぞれ記述された部分関数50.jpgの重ね合わせで記述する。
59.jpg
それぞれの部分関数51.jpgは、
79.jpg
のガウス型の基底関数で展開される。ガウス関数のサイズパラメータ（80.jpg,82.jpg）は等比数列により決める。
345.jpg、　　　　346.jpg
従ってガウス関数の個数とパラメータの最小・最大値（56.jpg,267.jpg,347.jpg）、（352.jpg,350.jpg,348.jpg）が入力するパラメータになる。この試行関数を用い変分計算を行う。この方法は基底関数間の一次独立性がよいため倍精度のベクトル演算が可能で短時間で計算できる。ハミルトニアン行列の大きさは3200次元程度（最大4200次元）で、計算時間は後述の種々の補正計算も含めてスーパーコンピュータFACOM VPP500で8分程度である。
全角運動量Ｊを持つpHe+３体系の準安定状態は、ヘリウムHe2+−p間の角運動量がＪ−4以下のpHe2++e-の２体の散乱状態よりもエネルギーが高くなる。従ってpHe+の準安定状態は真の束縛状態でなく、Feshbach型の共鳴状態である。但しこの場合e-が大きな角運動量を持ち去らなければならないため、幅は非常に小さいが（エネルギーに比べて10桁以上小さい）、高精度に計算するためには散乱の境界条件を考慮する必要がある。我々は試行関数中のサイズパラメータ521.jpgの変化に対するエネルギー固有値の振舞いから共鳴の中心と幅を決めた。サイズパラメータにスケール因子332.jpgを掛けて
330.jpg
繰り返し計算を行った。散乱の波動関数の寄与がほとんど無視できる、エネルギーの幅がエネルギーに比べて十分小さいとき、331.jpgを実数にとり（Stabilization法）、522.jpgに対する固有値の安定性から共鳴の中心を決め、共鳴の幅を見積もった。幅が無視できないときは、523.jpgを虚数に取り（Complex coordinate rotation法）散乱の波動関数を近似的に取り込み、固有値の524.jpgの絶対値に対する安定性から共鳴の中心を、偏角の変化に対する振舞いから共鳴の幅をそれぞれ計算した。今回の計算では一部の状態（例えばp4He+の(Ｊ,u)=(33,4)）を除いて幅が十分小さいので計算が容易なStabilization法を採用した。
図2のc=1とc=3の座標系はヤコビ型でないため、３体ハミルトニアンにそれぞれ質量分極項75.jpgが現れる。
574.jpg
原子核の質量78.jpgは電子に比べ大きいためこの寄与は小さいと予想されるが、組替えチャネルの計算においてこれを無視すると、サイズパラメータに対するエネルギー固有値の安定性が失われ連続状態のように振る舞う。これはチャネル間のハミルトニアンの違いにより、この方法により分離されるべき共鳴状態と、散乱状態の重ね合わせである疑似状態が混合したためと考えられる。

3. 相対論およびQED補正
次の(1)から(4)の相対論およびQEDの補正を非相対論波動関数533.jpgを使い一次の摂動論で計算した。準安定状態のエネルギー（〜3 a.u.）に対してそれぞれの補正項の寄与は以下の通りである。
(1) 電子の運動に対する相対論補正（パウリ近似）。この項の寄与は、-5×10-5 a.u.程度である。
95.jpg
(2) He2+およびpの運動に対する相対論的補正。この項の寄与は、-3×10-8 a.u.程度である。
96.jpg
(3) ラムシフト。311.jpgは平均励起エネルギーを表す。この項の寄与は、+1×10-5 a.u.程度である。
257.jpg
(4) ヘリウム原子核およびpの有限の大きさによるクーロン力の補正。等電荷分布を仮定し、He2+、pの半径をそれぞれ536.jpg、537.jpgにとった。この項の寄与は、+1×10-9 a.u.程度である。
258.jpg
(1)の補正（ΔEPauli）により遷移波長の実験値との差は10ppm程度に減少し、(3)の補正（ΔELamb）を加えることにより ppm程度に減少した。その他の補正は有効数字7桁の範囲では効かなかった。二次の摂動の寄与は10-10 a.u.程度でこれも無視できる。
図3.に相対論補正と平均粒子間距離のpHe+状態（Ｊ,u）依存性を示す。高励起状態ほどΔEPauliとΔELamb補正の値は大きくなる。これは高励起状態になるとHe2+−p間の距離が増大し、逆にp−e-間の斥力によりe-がHe2+に接近し、深く束縛して（電子の速度が増加する）、補正の値が大きくなると考えられる。
figure38
figure39

4. 結果
表1. 共鳴遷移波長の計算値および実験値。
  (Ｊi,ui)→(Ｊf,uf) l(Theory) (nm) l(Experiment) (nm)
Non-relativistic Relativistic and QED without Corrections with Corrections
p4He+
Dv=0		 (35,3)→(34,3) 597.2290 597.2573 597.259(2) 597.2570(3)
(34,2)→(33,2) 470.7048 470.7220 470.724(2) 470.7220(6)
(35,2)→(34,2) 529.5962 529.6188 529.622(3)  
(35,2)→(36,2) 597.2633 597.2927 597.298(2)  
(36,1)→(37,1) 597.3626 597.3934 597.397(2)  
(35,1)→(36,1) 528.7809 528.8042 528.808(2)  
(36,0)→(37,0) 527.9031 527.9272 527.930(2)  
(37,0)→(38,0) 597.5716 597.6041 597.607(2)  
p3He+
Dv=0		 (34,3)→(33,3) 593.3586 593.3873 593.388(1)  
(33,2)→(32,2) 463.9282 463.9455 463.946(2)  
(34,2)→(33,2) 524.1312 524.1541 524.155(4)  
p4He+
Dv=2		 (34,2)→(33,4) 726.021 726.092 726.097(3)  
(35,1)→(34,3) 713.5241 713.5816 713.578(6)  
表1.に共鳴波長の理論値と実験値（前述の実験グループによる）を示す。共鳴波長は、
344.jpg
の関係によって与えられる。ここで282.jpgを使った。右辺の分母の557.jpgの計算で桁落ちのため、表1.「l(Experiment) 」にある実験値（7桁の有効数字）と理論値を比較するにはエネルギーの計算で8桁以上の精度が必要になる。表1.の「Non-relativistic」はクーロン相互作用のみを用いた計算で、実験値との差は50ppm程度あった。相対論およびQEDの補正を加えた計算（表1.中「Relativistic and QED」）と実験（表1.中「with Corrections」）はppmの高精度で一致した。またpHe+と周囲のヘリウム原子の衝突に起因する「ヘリウム密度補正」のない場合（表1.中「without Corrections」）とは系統的に計算値が実験値と比べて小さい。密度補正のある２つの実験値とは実験誤差の範囲で一致した。これはこれまで知られていていた反陽子原子のエネルギーの理論・実験間の一致の記録を２桁向上したことになる。Korobovによる全く別の計算方法による結果と今回の計算結果は非相対論および補正計算ともよく一致している。
今回の計算ではHe2+の質量は7294.299 a.u.、pの質量はpと同じ1836.1527 a.u.を使った。共鳴波長に対するpの質量依存性を調べpとpの質量の対称性を検討するため、pの質量をpの質量から微少量528.jpgだけシフトさせる。
270.jpg
pとpの比電荷は10-9の精度で等しいことがpとpのサイクロトロン周波数による比電荷の測定から分かっているため、pの電荷も同時にシフトさせる。
527.jpg
このようにシフトされた定数を使い共鳴波長をもう一度計算し、pの質量（同様に電荷）のpからのずれを評価する。密度補正を含む実験値の誤差542.jpgと図4.の傾きから532.jpgを見積もった。
294.jpg

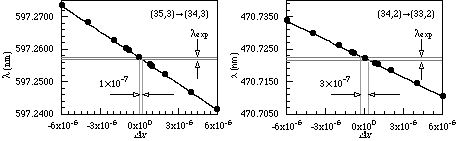
559.jpg
図4. 共鳴波長に対するシフト値310.jpg依存性。●は計算値。

5. まとめ
「非断熱組換えチャネル結合変分法」を使い反陽子ヘリウム原子の準安定状態のエネルギーと共鳴波長の計算を行った。相対論およびQEDの補正を加えた計算結果は実験値と1ppm以下の精度で一致し、この方法は、大きな角運動量（Ｊ〜35）を持ち、また原子と分子の二面性を持つエキゾチックな３体系も高速で精密に計算できることを示した。共鳴波長に対するpの質量と電荷の依存性は比電荷とは異なるため、これとは別にpとpのの質量（または電荷）に対してその対称性が10-7の精度で成り立つことを示した。
今後さらに高精度のpHe+の理論・実験の比較により、量子力学的３体問題の解法、（多体系における）相対論・QED効果の精密計算、粒子・反粒子の質量・電荷の対称性の検証等の研究が期待される。




戻る,