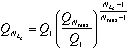組替えチャネル結合法による反陽子ヘリウム原子準位と反陽子質量の精密計算
木野康志
東北大学大学院理学研究科化学専攻
1. はじめに
陽子の反粒子である反陽子（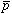
）は、通常物質中に打ち込まれるとps程度の間に消滅してしまうが、ヘリウム中に打ち込まれた
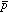のうち約3パーセントが106倍も長い寿命（数ms）を持つ（但し残りの97%はpsの速さで消滅する）。
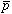はヘリウム（He）中に打ち込まれると、Heとの衝突により次第にエネルギーを失い、最後にHe中の電子（
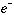）と入れ替わり反陽子ヘリウム原子
（
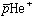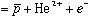）を形成する。
この際、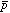
は入れ替わる
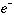とほぼ同じ半径（またはエネルギー）をもつ軌道に入る確率が高いと考えられている。そのため
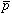の主量子数nは、
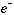と
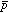の質量の違いから、
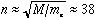程度の値をもつ（M、
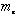はそれぞれ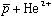
、
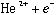の換算質量）。このうち大きな軌道角運動量（>30）を持つ
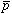は、遠心力により
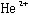に近づけず原子核による吸収を免れ準安定状態となる。この状態では
−
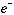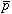間の強い相関により
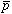の角運動量状態に対する縮退は解け、
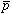は遅い電磁遷移により脱励起し、その後残りの
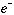を弾き出し(Auger崩壊)、
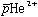の水素様原子になる。二体系の
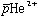の角運動量状態は縮退しているため、周りの
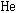との衝突で速やかに角運動量を失い （Stark混合）、
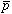は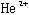
と接触し原子核に吸収され消滅する。電磁遷移が支配的な準位は長い寿命を持ち、Auger崩壊が支配的な準位は短い寿命を持つ。現在、欧州合同原子核研究機関（CERN）の反陽子減速器（Antiproton Decelerator; AD）においてこの二種類の状態間の精密な
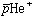のレーザー分光実験が行われている（鳥居寛之氏の概要を参照されたい）。実験において
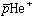の生成量は極く僅かで、レーザーのバンド幅も狭いため予め理論計算によるレーザーの共鳴振動数を知ることがが不可欠でる。我々は独自の方法（組替えチャネル結合法）を開発し、この共鳴振動数の計算を行っている。現在実験値と理論値の差は10 ppbのオーダーに達し、
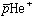の精密分光により比電荷の測定とは別の見地で
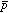と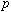
の質量（または電荷）の対称性を探ることが可能となった。
2. 計算法
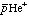は、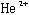
（Z=+2）の周りを
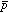（Z=-1）と
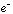（Z=-1）が回る「ヘリウム原子的」な描像と、圧倒的に重い
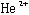と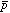
の周りを軽い
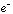が回る「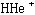
分子的」な描像が同時に成り立つ奇妙な三体系である。また
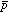と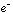
間の相関も重要な役割を果たす。「原子的描像」「分子的描像」および「
−
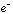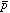相関」を同時にかつ直接計算に取り入れるため、全波動関数
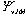を図1.に示す3つの座標系でそれぞれ記述された部分波動関数
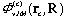の重ね合わせで記述する。（組替えチャネル結合法）
それぞれの部分波動関数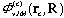
は、
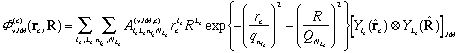
のガウス型の基底関数で展開される。近距離での粒子間の相関と遠距離での波動関数の振舞いを効率良く再現するため、ガウス関数のサイズパラメータ（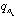
,
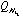）は等比数列により与えられる。
、
,
,
）、（
,
,
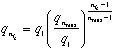
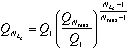
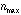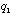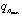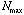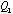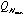）が入力するパラメータになる。この試行関数を用い変分計算を行う。この方法は基底関数間の一次独立性がよいため倍精度のベクトル演算が可能で短時間で計算できる。ハミルトニアン行列の大きさは3200次元程度（最大4200次元）で、計算時間は後述の種々の補正計算も含めてスーパーコンピュータFACOM VPP500で8分程度である。現在我々と同精度の計算がロシアのKorobovらによってなされているが、彼らの計算では、一つのエネルギー準位の計算に20時間かかる。この違いは我々の方法では波動関数を記述する基底関数間の直交性がよいため、言い換えると基底関数が物理的性質をよく表現しているため、エネルギー固有値を求める際の対角化で桁落ちが起こりにくいため倍精度計算が可能になりスーパーコンピュータにより高速に計算できる。一方Korobovらは基底関数間の直交性が悪いため4倍精度計算が必要である。計算が短時間に行えるため後述の複素座標回転法や、
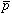の質量や電荷をパラメータにしてエネルギー準位の計算を再度行い、
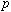と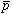
の対称性を評価することが出来た。また、この計算では
−
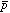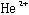間の大きな軌道角運動量（〜35）を取り扱うため、角運動量代数の計算の際大きな数同士の掛算、割算が必要になり、数値計算において各所で桁あふれ(over/under flow)が生じるが、計算の順番を工夫することによりこれを克服した。
全角運動量Ｊを持つ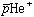
３体系の準安定状態は、ヘリウム
−
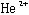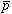間の角運動量がＪ−4以下の
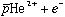の散乱状態よりもエネルギーが高い。従って
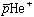の準安定状態は真の束縛状態でなく、Feshbach型の共鳴状態である。但しこの場合
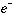が大きな角運動量を持ち去らなければならないため幅は非常に小さいが、高精度に計算するためには散乱の境界条件を考慮する必要がある。我々はこの効果を取り入れるため複素座標回転法を用いた。複素座標回転法においては、座標は
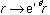のように変換される。この変換により変換されたハミルトニアンの複素固有値
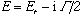から共鳴状態のエネルギー
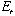と幅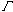
を求めることができる。Eは、
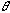によって変化するが、共鳴状態に達すると変化しなくなる。
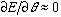。我々は更に実数パラメータ
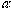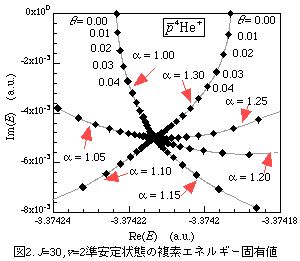
により座標を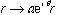
のようにスケールしEの収束性を確かめた（図2）。この方法では厳密な境界条件を必要とせずに遠方での波動関数の振動成分を近似的に取り込むことができる。ここで大次元の複素行列の一般固有値問題を多数計算する必要になるが、我々の方法では一つの固有値を高速に計算することができ、更に計算のパラレル化（同時に複数のCPUで演算を行う）を行うことにより、例えば図2.の全ての計算は8 CPUの場合5時間で計算が可能である。
3. 相対論およびQED補正
次の(1)から(4)の相対論およびQEDの補正を非相対論波動関数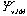
を使い一次の摂動論で計算した。準安定状態のエネルギー（〜3 a.u.）に対してそれぞれの補正項の寄与は以下の通りである。
(1) 電子の運動に対する相対論補正。この項の寄与は、-5×10-5 a.u.程度。
(2) 
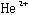および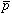
の運動に対する相対論的補正。この項の寄与は、-3×10-8 a.u.程度。
(3) ラムシフト。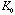
は平均励起エネルギー。この項の寄与は、+1×10-5 a.u.程度。
(4) ヘリウム原子核および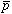
の有限の大きさによるクーロン力の補正。等電荷分布を仮定し、
、
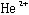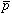の半径をそれぞれ
、
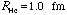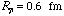にとった。この項の寄与は、+1×10-9 a.u.程度。
(1)の補正により遷移波長の実験値との差は10ppm程度に減少し、(3)の補正を加えることにより ppm以下に減少した。二次の摂動の寄与は10-10 a.u.程度でありこれは無視できる。
図3.に相対論補正と平均粒子間距離の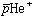
状態（Ｊ,u）依存性を示す。高励起状態ほど補正の値は大きくなる。これは高励起状態になると
−
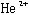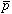間の距離が増大し、逆に
−
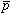間の斥力により
-が
に接近し、深く束縛して（電子の速度が増加する）、補正の値が大きくなると考えられる。
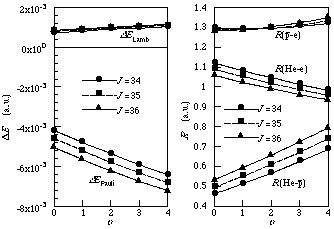
図3. 補正項(左)と平均粒子間距離(右)の状態（Ｊ,v）依存性。
4. 結果
表1.に理論値と2000年夏に行われた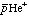
の最新の共鳴振動数の実験値（Phys. Rev. Lett. 印刷中）を示す。理論値と実験値は最高21 ppbの精度で一致した。現在この三体系に関する理論計算で世界最高の精度をもつのは、我々とロシアのKorobovらによる計算である。二つの理論計算は全く異なる方法で行われているが、7桁以上の精度で一致している。ただし(34,1)→(33,3)の遷移において我々の計算のみが実験値を正しく予言することが出来た（Korobov: 486141 GHz）。これは娘準位(33,3)が隣接する同じ軌道角運動量とパリティをもつ短寿命状態と強く結合するためである。図3. に(33,3)状態と短寿命状態の構造図を示す。二つの状態の幾何学的構造は大きく異なるが、二つの状態を同時に取り込んだ計算を行わなければ精密なエネルギー準位は求めることが出来ない。実験結果は我々の計算の方がより精密にこの三体系を計算できる事を示している。表2.にAuger崩壊率を示す。(33,3)状態については我々以外の理論値は実験値から大きく外れている。我々と実験値との不一致は単寿命状態が周囲のHeにより圧縮される効果であると推測している。実際単寿命状態の半径を制限すると実験値を再現する。
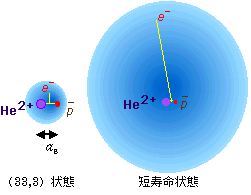
図4. (33,3)状態と短寿命状態の構造図。
表1. 共鳴遷移振動数、J、vは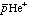
の回転、振動の量子数、括弧内の数字は計算または実験の誤差。
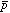の量子数
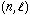とは、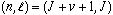
の関係にある。
 |
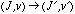理論 (GHz) |
実験 (GHz) |
差 (ppm) |
 |
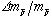| (33,1)→(32,1) |
804633.127(5) |
804633.11(11) |
0.021 |
5.41×10-8 |
| (32,0)→(31,0) |
1012445.559 |
1012445.52(17 |
0.039 |
9.44×10-8 |
| (35,3)→(34,3) |
501948.828(8) |
501949.01(13) |
-0.36 |
-1.61×10-6 |
| (35,1)→(34,3) |
412885.131(8) |
412885.18(12) |
-0.12 |
-7.18×10-7 |
| (34,2)→(33,4) |
420121.53(1) |
420121.9(10) |
-0.88 |
-2.40×10-6 |
| (34,1)→(33,3) |
486104.43(7) |
486102.6(7) |
3.8 |
1.28×10-5 |
表2. Auger崩壊率λ(s-1)と寿命τ(s)、τ=λ-1。
 |
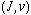λ(木野) |
λ(Korobov 島村) |
τ(木野) |
τ(実験) |
| (33,3) |
4.41×1010 |
5.7×109 |
2.26×10-11 |
(1.1±0.3)×10-11 |
| (33,4) |
3.08×1011 |
3.1×1011 |
3.25×10-12 |
(4.1±0.2)×10-12 |
| (33,3) |
1.84×108 |
2.2×108 |
5.45×10-9 |
(5±1)×10-9 |
これまで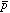
の質量や電荷に関してはそれぞれ単独で精密に測定されていなかった。
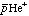のレーザー共鳴波長から
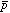の質量（または電荷）の不確定さを推定することが出来る。理論計算上で
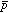の質量を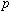
の質量から微少量
だけシフトさせ計算を行う。
但しと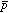
と
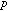の比電荷（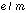
）は10-9の精度で等しいことが
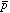と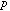
のサイクロトロン周波数による測定から分かっているため、
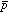の電荷も同時にシフトさせる。
このようにシフトされた定数を使い共鳴波長をもう一度計算し、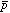
の質量（同様に電荷）の
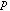からのずれを評価する。実験値と理論値の差
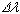と図4.の傾きからずれ
を見積もった。
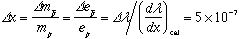この結果はこれまでの反陽子原子の分光精度を2桁以上向上したことになり、2年毎に更新されている素粒子リスト「Particle Data Group（Eur. Phys. Jour. C15. 1 (2000), http://pdg.lbl.gov）」に採用された。表1.に最新の
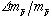を示す。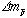
の精度は複素座標回転法による新しい計算値とADにおける新しい実験値により更に1桁更新された。
最近我々は、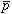
の磁気双極子能率を求めるため
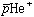の超微細構造の計算を行った。計算結果とKorobovらの最新の結果と20 ppmの精度で一致した。従来の
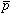の磁気双極子能率は0.3 %の低い精度でしか求められていなかったが、我々の計算値と、これからADにおいて行われるレーザーマイクロ波共鳴分光法を用いて
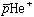の超微細構造の精密測定との比較によりa2=50 ppmの精度で
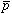の磁気双極子能率が決定できる。これにより
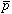と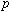
の内部構造に関する対称性を検証できると期待される。
5. 謝辞
本研究は、上村正康氏（九州大）、山中信弘氏（東京大）、工藤博司氏（東北大）、Piotr Froelich氏（Uppsala大）との共同研究により行われました。山崎敏光氏（理研）、早野龍五氏（東京大）、鳥居寛之氏（東京大）、堀正樹氏（CERN）、石川隆氏（東京大）、山崎泰規氏（東京大／理研）のASACUSA実験グループには発表前の最新の実験データの提供していただき、深く感謝します。また、V.I. Korobov氏（JINR）、D.D. Bakalov氏（Bulgarian Acad. of Sci.）、G. Korenman氏（Moscow大）、島村勲氏（理研）、大槻一雅氏（電通大）には理論計算について議論していただきました。数値計算は理化学研究所スーパーコンピュータFACOM VPP700Eで行われました。
戻る,
