特異値分解による物理系の自動的特徴抽出に関する研究
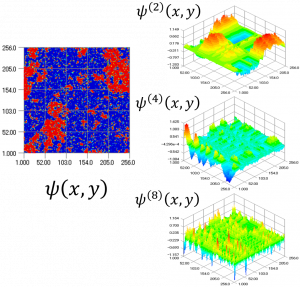
特異値分解による2次元強磁性スピン模型のスナップショット解析
「特異値分解」は,主成分解析・特徴抽出のアルゴリズムの一つとして,情報処理分野ではよく知られています.一方,物理の分野においても,この方法は量子多体系の「エンタングルメント(量子もつれ)」の精密な表現のために活用されてきた経緯があります.特異値分解を様々な物理の問題に応用することで,どのようなメカニズムで対象とする系の重要な情報を自動抽出できるのかを明らかにすることが重要です.その理解を深めるための研究を推進しています.物理分野では,系の特徴抽出法として「くりこみ群」が極めて重要な視点であり,くりこみと特異値の間にどのような関係があるのかを理解したいということが最も重要なポイントです.
実際に,古典統計模型の特異値解析を通して,相転移の臨界現象やくりこみ群理論に関わる深い理解が得られることが分かってきました.また,特異値分解とウェーブレット解析の繋がりも得られています.ウェーブレットはJPEG等の情報圧縮に使われている数学です.更には,物理の視点から得られた特異値分解の性質を逆に活用して,ニューラルネットや人工知能の機能解析を行うことができることも分かっています.これらは古くはスピン系の物理から派生したものであり,情報と物理が交錯する異分野横断的テーマとなっています.
量子古典変換

熱場の量子論による有限温度状態のテンソルネットワーク表現とBTZブラックホールの対応
「量子古典変換(ホログラフィー原理,バルク・境界対応)」と呼ばれる概念を指導原理として,次世代物理の統合理論を構築しようという野心的な試みが素粒子論分野において推進されています.これは取り扱いの難しい空間d次元の場の量子論の問題が,空間(d+1)次元の古典的一般相対論と等価であるという非常に驚くべき予想です.このことは,例えば,空間3次元ではもつれのないグラフを空間2次元に射影すると特異点が現れることと似ています.量子側のエンタングルメントと古典側の時空の幾何学に深い関連があることが指摘され大きな興味を持たれていますが,どのような場合にこのような非自明な変換が起こるのかという数学的背景は未だ完全には解明されていません.
私達の研究のオリジナルなアプローチ法は,これを量子情報のメモリの問題と捉えることです.すなわち,量子系などの複雑系の相関関数の情報を適切なフォーマットで表現し,それを情報量最小で格納できるメモリ空間を構成します.このメモリ空間の幾何学がユークリッド幾何学ではなくリーマン幾何学であり,相関長の異なる情報が時空の異なる場所に最小の情報量で格納され,それがあたかも古典的な場として振舞います.この結果,元の系の状態方程式がアインシュタイン方程式に変換されます.これを実際に表現するための数学的研究を行っており,例えば,有限温度の量子系のエンタングルメントの情報から古典側のブラックホール解が構成できるなどの成果を得ています.
今後は時間発展の問題に主眼を置きたいと考えており,それを具体的に推進するために,量子アルゴリズムの量子古典変換にも注目しているところです.
量子多体論
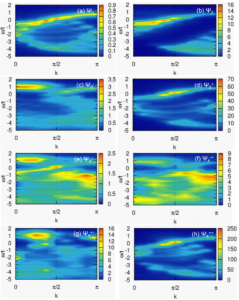
キャリアドープしたMott絶縁体の複合励起スペクトルの解析
物性物理学では,「量子多体問題」の解明は長年の大きな懸案課題です.ここで主題となるのは超伝導や磁性などの電子状態ですが,一電子近似が可能な半導体と異なり,それらは電子間の多体相互作用による新規な秩序から生じます.精密な電子状態解析のために,系の持つエンタングルメントや非局所励起の性質を正確に取り込めるような理論およびテンソルネットワーク法や密度行列くりこみ群法の数値計算アルゴリズム開発を行っています.
これまでは銅酸化物高温超伝導体の電子状態や,低次元遷移金属酸化物の光物性,光誘起相転移の問題などを取り扱ってきました.今後は,金研中性子グループや東北放射光とも連携して,量子ビームによる高度な物性測定に関わる理論構築を進めていきたいと考えています.
また,量子多体論の技術・研究方法を量子情報分野にも応用していきたいと考えています.量子情報処理といえば量子コンピュータや量子通信を真っ先に思い浮かべる方が多いかもしれませんが,物理の観点からは,これらは量子スピン系のエンタングルメント・ダイナミクスや光と量子二準位系の相互作用の問題と非常に相補的なものです.量子スピンを量子ビットとみなせば,一斉制御可能な量子ビットの空間スケールや情報の伝送速度,環境への散逸・不純物・欠陥などによるデコヒーレンスや相転移,具体的にアルゴリズムを乗せて動作させたときの計算の安定性や精度補償の問題など,多くの課題を取り扱うことができると思われます.
